Praktická cvičení z Numerické matematiky

Numerické řešení PDR - 10. týden

  • Dirichletova okrajova uloha pro Poissonovu rovnici (MATLAB)

    • Oblast: ctverec [0,1]^2, okrajova podminka phi(x,y) = 0, prava strana f(x, y) = sin(pi x) sin(pi y).

    n = 11; 
e = ones(n,1); 
T = full(spdiags([-e 4*e -e ], [-1:1], n, n)); 
E = diag(-e);
A = []; for i = 1:n, A = blkdiag(A, T); end,
A = A - diag(ones(n*(n-1),1), -n) - diag(ones(n*(n-1),1), n);
    Sestavime pravou stranu:

    
[xx, yy] = meshgrid((1:n)'/(n+1), (1:n)'/(n+1));
h = 1 / (n + 1);
b = h * h * sin(pi * x) * sin(pi * y);
b = reshape(b, n * n, 1);
    Reseni soustavy a zobrazeni reseni:

    
u = A \ b;

uu = reshape(u, n, n);

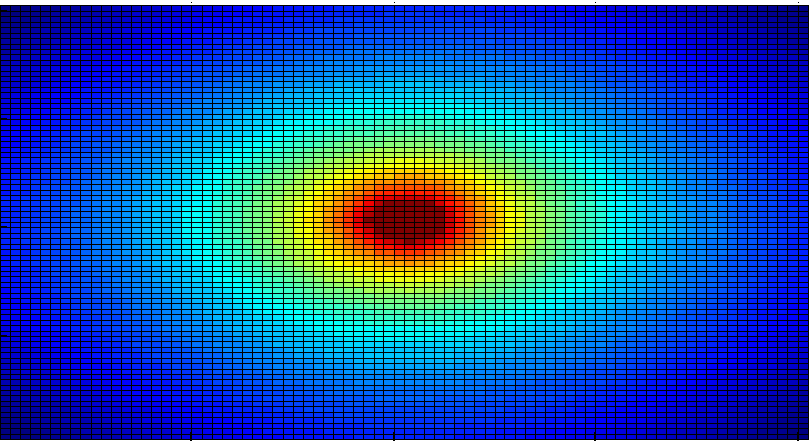
mesh(xx, yy, uu);
  • Dirichletova okrajova uloha pro Poissonovu rovnici (Jazyk C)

    • Uloha: - Laplace u = f, Oblast: ctverec [0,1]^2,
    Okrajova podminka: u = 0,
    f(x, y) = sin(pi x) sin(pi y).
    Opravte si n = 10 v programu (dle potřeby)
    Zde soustavu rovnic nesestavujeme jen resime (viz 3. cviceni). 

    for(i = 1; i < n; i++)
 for(j = 1; j < n; j++)
   U[i][j]=(b[i][j]+U[i-1][j]+U[i+1][j]+U[i][j-1]+U[i][j+1])/4.;
    Celý program poisson2d.c

    Zobrazeni vysledku v MATLABu 
    load sol.dat;
mesh(sol);
    Zobrazeni vysledku v GNUPLOTu 
    sp "sol.dat" matrix with linepoints

  • Poissonova rovnice Neumannovou okrajovou podminku na casti hranice (Jazyk C)
    • Uloha: - Laplace u = f, Oblast: ctverec [0,1]^2,
    Okrajova podminka: u = 0   pro x = 0 nebo   du/dn = 0 jinde
    f(x, y) = sin(pi x) sin(pi y).
    Opravte si n = 10 v programu.
    Zde soustavu rovnic nesestavujeme jen resime (viz 3. cviceni).



    Celý program poisson2d_neumann.c

  • Poissonova rovnice (stacionarni problem vedeni tepla / jazyk C)

    • Jedna se o ukazku, jak i s takto jednoduchou metodou je mozne spocitat zajimavy priklad: zde uvazujeme potrubi jimz proudi horka kapalina (vnitrek kruhovy prurez, vnejsi ctverec - z duvodu realizace Neumannovy okrajove podminky), potrubi teplo vede a dochazi k prestupu tepla do okolniho prostredi o urcite teplote. Parametry neodpovidaji realne situaci, jedna se jen o cvicny priklad.
    Celý program potrubi.c

    Zobrazeni vysledku v GNUPLOTu 
    sp "sol.dat" matrix with linepoints