ENZYMES

The primary structure of proteins can also be changed, decomposed into shorter chains or even into basic amino acids, either by the action of strong chemical agents (e.g., sulphuric acid) or by other kinds of proteins. The decomposition is called hydrolysis, and the protein that is able to cleave a polypeptide chain is protease - an enzyme. Enzymes are proteins that catalyse a wide spectrum of chemical reactions, see Tab.11.2. (the suffix -ase)

Class Reaction catalysed
Hydrolases Hydrolysis: cleaving proteins (proteases), nucleic acids (nucleases), saccharides (carbohydrases)
Oxidoreductases Addition of oxygen or removal of hydrogen to or from a substrate (oxidases, dehydrogenases)
Transferases Transfer of functional groups (transaminases, transmethylases, etc.)
Lyases Catalyze the elimination of groups to form double bonds
Isomerases Conversion of isomers (e.g. the enzyme glucose isomerase converts glucose to fructose)
Ligases Formation of new bonds (ligases are used in genetic engineering when forming artificial DNA)

A remarkable feature of enzymes is their selectivity, i.e., each enzyme acts only on a specific substance, which is recognised according to its shape (a lock and key concept: the reactant /substrate S/ is a key which must fit into a lock, an enzyme E). The mechanism of the enzyme catalysed reaction E+S>ES>E+P is demonstrated in Fig.11.5. It may happen that the enzy me E mistakes the reactant S for a substance F having a similar shape, E+F>EF. Then the "foreign" substance occupies a portion of the active sites on the enzyme surface, the reaction slows down, and we say that the activity of the enzyme is inhibited (competitive inhibition).

We will try to analyse the kinetics of the fermentation process, i.e., to derive a rate equation based on the lock and key theory. First, we describe the situation at a particular time t in terms of concentrations [S], [P], [E], [F], [ES], [EF] (i.e., by the number of molecules of S-substrate, P-product, E-free enzymes, F-inhibitor, ES, EF- activated complexes). Then we estimate the changes in concentration during a short time interval (t, t+dt).
In words: The number of molecules S (substrate) is diminished by the number of molecules which adhere to a free enzyme E. This amount is directly proportional to the concentration of S and to the number of free enzyme sites [E]. On the other hand, the reverse reaction ES>E+S increases [S] proportionally to the concentration [ES]. Written as an equation these sentences go like this
(11.1)
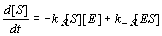The number of molecules F is also diminished during the time interval dt by the enzyme lock EF, though this need not be for ever. There is always a certain probability that the locked molecules F will escape and this probability is given by a constant k-F
(11.2)
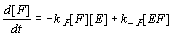Assuming that each activated complex ES decomposes into a constant number of molecules P we can write
(11.3)
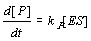Changes of [ES] correspond to the three reactions E+S>ES, ES>E+S, ES>E+P:
(11.4)
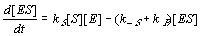Similar equations might also be written for [EF] and [E], but it is easier to replace them by the two constraints
(11.5-6)
where [E]0 and [F]0 are initial concentrations at the beginning of a process (e.g., at the beginning of batch fermentation). Only now does the number of unknown concentrations [S], [P], [E], [F], [ES], [EF] agree with the number of equations. The system is complete and can be solved in a similar way as the gas lighter in Chapter 7. Assuming that the inhibitor concentration [F] is negligible, system (11.1-6) can be reduced to the two following equations for two unknowns [S] and [ES] :
(11.7-8)
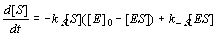
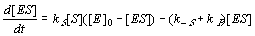If the rate of the activated complex changes is also negligible (d[ES]/dt=0), the concentration [ES] can be eliminated from Eqs. (11.7-8), giving the equation
(11.9)
where kM=(kP+k-S)/kS. "Nihil novi sub sole", Eq.(11.9) was formulated by Leonor Michaelis and Maud Menten in 1913.
It is interesting to compare the M-M equation (11.9) with the Monode equation (8.70), which describes biomass growth.

Solution of Eqs.(11.1-8), was prepared in the following Excel table (the same procedure was used in Example 7.3). Row 8 is a header, initial concentrations are prescribed in row 9, and row10 is the first time step. For example column B follows from Eq.(11.9):[S]1=[S]0-dt kP[E]0 [S]0 /(kM+[S]0):

Atime B [S] (11.9) C [S] (11.1) D [ES](11.8) E [P](11.3) F [F](11.2) G [EF] H [E]
0 =s0 =s0 =0 =0 =f0 =0 =e0
=A9+dt =B9-dt*kp*B9*e0/ (kmm+B9) =C9+dt*(kms*D9- ks*C9*H9) =D9+dt*(ks*C9*H9- (kms+kp)*D9) =E9+dt*kp*D9 =F9+dt*(kmf*G9 -kf*F9*H9) =f0-F10 =e0-D10- G10

Subsequent rows 11,12,13,...., i.e. time steps 2,3,4,.... are only an extension of row 10. Typical results, time courses of the substrate concentration according to Eq.(11.9) and (11.1), are shown in Fig.11.6.



@TEC: 3. 3.2003 Change language to English DEFAULT BACKpeoples U218 FS-CVUT Interesting links mailto: Zitny