System of nonlinear equations F(X) = 0

Newton's method

Problem 1: Find the solution of the nonlinear system
x2 = x13 + 1
x12 + x22 = 4

Graphical solution: 
>> ezplot('x_1^2 + x_2^2 - 4')
>> hold on
>> ezplot('x_2 - x_1^3 - 1')

Numerical solution: First of all, transform the system to the form F(X) = 0,
where X = [ x1 , x2 ]T, F = [ f1(X) , f2(X) ]T :
f1(X) = x12 + x22 - 4 ,
f2(X) = x2 - x13 - 1 .

Using Matlab, define F as

>> syms x1 x2          % define symbolic variables x1, x2
>> XV = [ x1 ; x2]     % vector of the variables x1, x2
>> f1 = x1^2 + x2^2 -4 % function f1 of x1, x2
>> f2 = x2-x1^3-1      % function f2 of x1, x2
>> F = [ f1 ; f2 ]     % vector function F of x1, x2

Jacobi matrix of F: 

>> J = jacobian(F, XV)

Choose a first approximation X: 

>> X = [1; 2]

Repeat following 4 commands: 

>> JX = subs( J, {x1, x2}, {X(1), X(2)})  % substitute a value of X to J
>> FX = subs( F, {x1, x2}, {X(1), X(2)})  % substitute a value of X to F
>> D = - JX \ FX                          % solve linear system JX * D = - FX
>> X = X + D                              % upgrade the approximation X

For Octave without symbolic variables 

  F = @(x) [x(1)^2+x(2)^2-4; x(2)-x(1)^3-1];
  dF = @(x) [2*x(1) , 2*x(2); -3*x(1) , 1];  % Jacobi matrix of F

  X=[1; 2];
  K = 3;
  for k=1:K
    d = -dF(X)\F(X);
    X = X+d;
  end

  printf('\nResult of X after %d iterations: \n', K);
  disp(X)
  printf('\nF(X): \n');
  disp(F(X))



Fixed point iterations

Solving the Problem 1 using fixed point iterations.

Define F as above:

  F = @(x) [x(1)^2+x(2)^2-4; x(2)-x(1)^3-1];

  alfa = 0.1; % for improvement of convergence - a guess
  G = @(X) X - alfa*F(X);  % transformation of F(x) = 0 to x = G(x)

  X=[1; 2];
  K = 30;  % converges much more slowly than Newt. meth.
  for k=1:K
    X = G(X);
  end

  printf('\nResult of X after %d iterations: \n', K);
  disp(X)
  printf('\nF(X): \n');
  disp(F(X))

Experiment with different values of maxit (number of iterations), X (the first approximation) and alfa (the coefficient influencing convergence).

Solve a similar problem with second equation changed to

x2 = sin(x1) + 1

so that 

  F = @(x) [x(1)^2+x(2)^2-4; x(2)-sin(x(1))-1];

(now the better choice of the parameter alfa would be 0.25)


Problem 2: Newton's method - illustration of basins of attraction

Consider the nonlinear system
x13 - 3 x1 x22 - 1 = 0
3 x12 x2 - x23 = 0
which has three solutions:  [1,0],   1/2 [-1, 31/2]   and  1/2 [-1, -31/2].

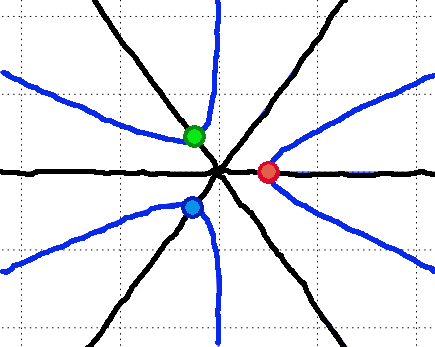
They can be found inside the three largest areas on the picture bellow: red, green and blue, respectively. For starting point at any colored area, Newton's method converges to the solution of the corresponding color (for example if the starting point lies at any of the red areas, Newton's method will converge to the solution [1,0]).

Julia set for the rational function

For more detailed explanation, see here.


Problem 3: Comparison of Fixed point iterations and Newton's method

Consider the nonlinear system

x1-1- x22 = 0
x2 + 2 x12 = 4

which has three solutions (after rounding to 5 decimal places, black dots):

P1=[0.06275, 3.99213],   P2=[1.24580, 0.89595],   P3=[1.54972, -0.80329],

and use four different starting points (red dots)

Q1=[0.125, 3.5],   Q2=[1.2, 1],   Q3=[0.75, 0.5],   Q4=[1, -1].

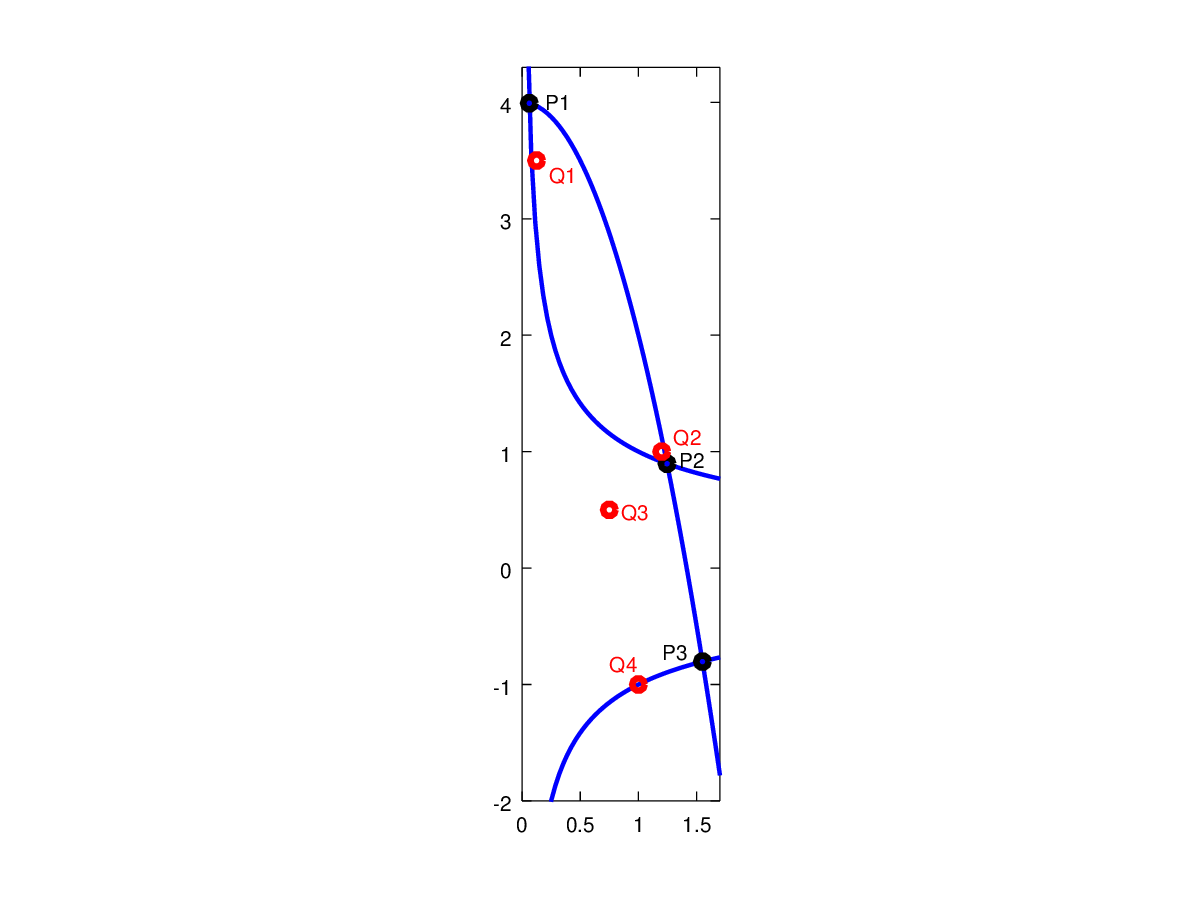
For each method and starting point, resulting point and a number of iterations are listed (with accuracy to 5 decimal places):

Method Q1 Q2 Q3 Q4
Newton's     P1 (12)     P2 (2)     P3 (5)     P3 (4)  
Fixed point iter.     P1 (7)     P1 (10)     P1 (8)     P1 (10)  

(For Fpi, the rearrangement x1 = x2-2,   x2 = 4 - 2 x12   was used.)