Počítačová grafika
2023/24
Mgr. Marta Hlavová
marta.hlavova@fs.cvut.cz
konzultace: čtvrtek 12:30-14:00, KN:D-304
konzultace: čtvrtek 12:30-14:00, KN:D-304
informace o předmětu → mat.fs.cvut.cz + Moodle
- obsah přednášek a cvičení
- podrobný harmonogram přednášek a cvičení
- literatura:
- Linkeová, I.: Základy počítačového modelování křivek a ploch
- klasifikovaný zápočet (dvě povinné plus jedna povinně volitelná práce,
odevzdávání v Moodle)
Rhinoceros 3d - verze 7
Počítačová grafika 2023/24

Křivka
podle hlediska:
- fyzika $\rightarrow$ dráha bodu
- geometrie $\rightarrow$ množina bodů dané vlastnosti - průnik, řez, ...
- matematika $\rightarrow$ spojité zobrazení intervalu do roviny či prostoru
- počítačová grafika $\rightarrow$ objekt generovaný řídícími/definičními body
Definice:
Křivka $=$ každá souvislá podmnožina $k$ prostoru $\mathbb{R}^n$, která je spojitým zobrazením intervalu $I\subset\mathbb{R}$.
Křivka $=$ každá souvislá podmnožina $k$ prostoru $\mathbb{R}^n$, která je spojitým zobrazením intervalu $I\subset\mathbb{R}$.
Křivka - analytická reprezentace
- explicitní $$y=\pm\sqrt{1-x^2}; x\in [-1,1]$$
- implicitní $$x^2+y^2=1$$
- parametrické $$x(t)=\cos{t},y(t)=\sin{t}; t\in [0,2\pi]$$
- bodová rovnice $$P(t)=[x(t),y(t)]; t\in I$$
- vektorová rovnice $$P(t)=(x(t),y(t)); t\in I$$
Křivka - analytická reprezentace
typ rovnice:
- transcendentní
- algebraická (polynomiální)
$$x(t)=\frac{1-t^2}{t^2+1}, y(t)=\frac{2t}{t^2+1}, t\in\mathbb{R}$$
Křivky v počítačovém modelování
interpolační
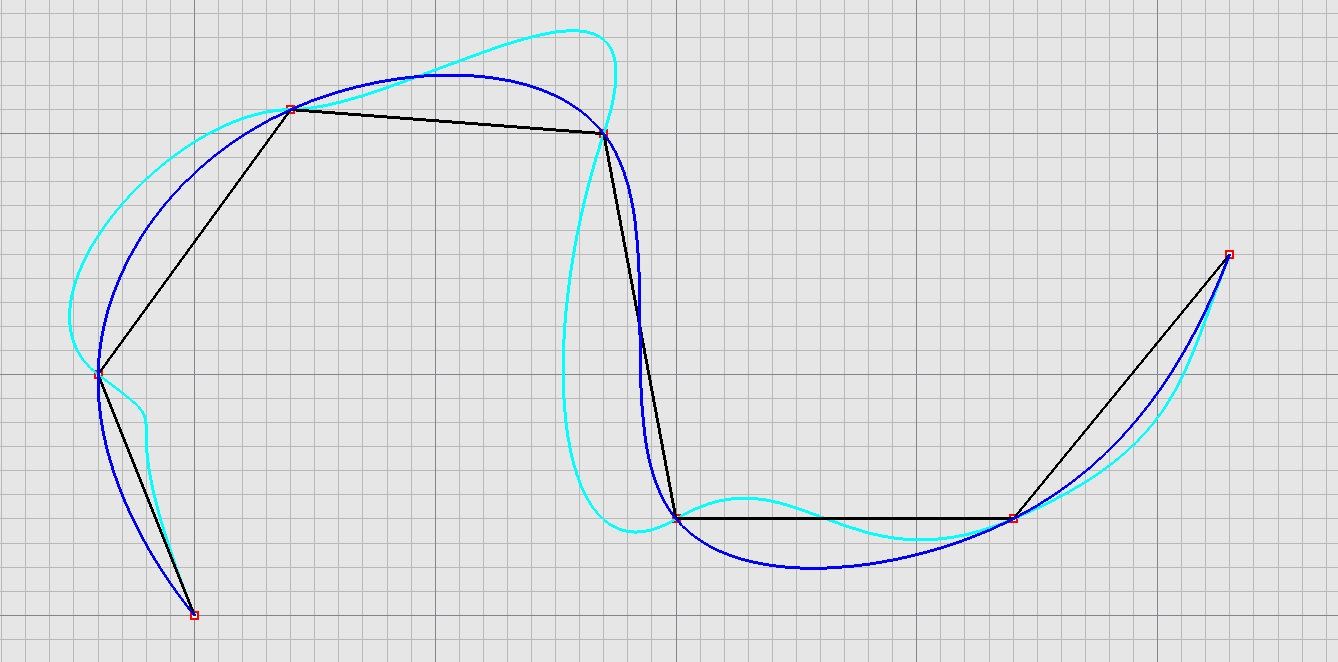
Fergusonova (Hermitova) kubika, spline křivky
Křivky v počítačovém modelování
aproximační
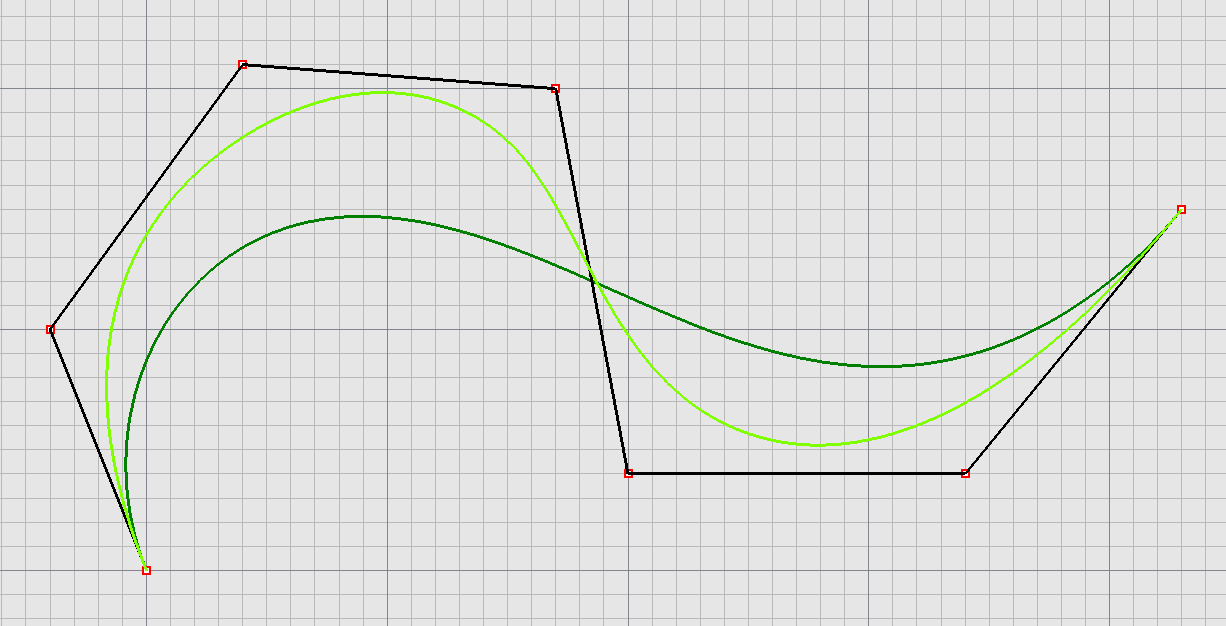
Bézierova křivka, Coonsova kubika, B-spline křivky, NURBS
interpolační vs. aproximační
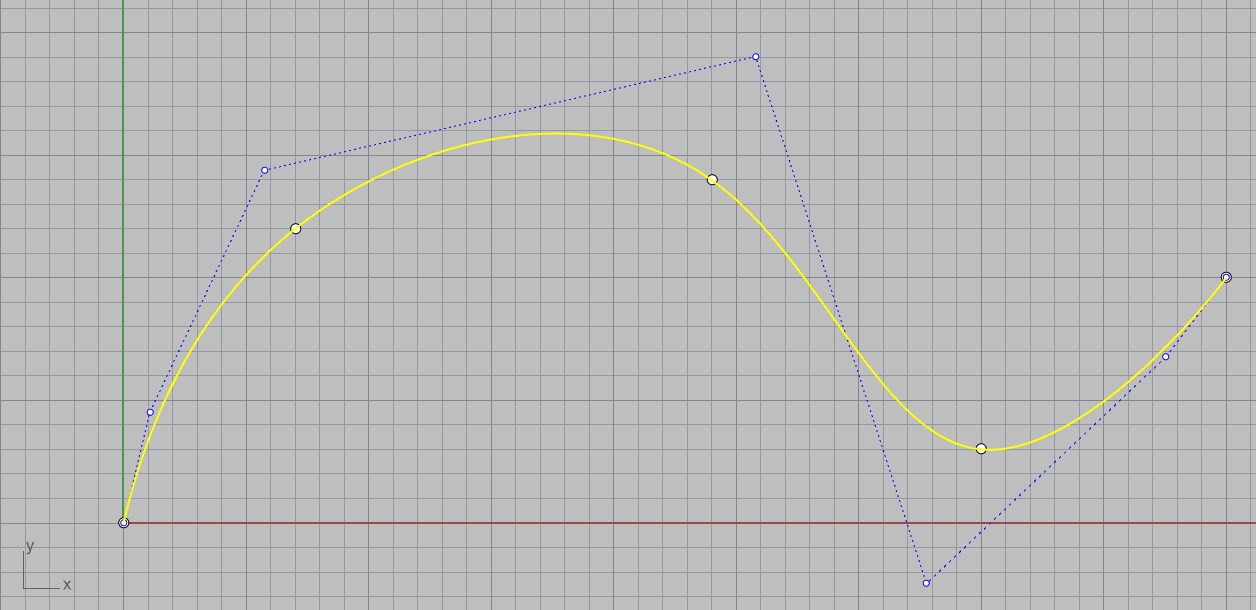
Základní pojmy
- segment, uzel
- uniformní parametrizace
- tečný vektor
- regulární (singulární) bod
- inflexní bod
Bézierova křivka n-tého stupně
Pierre Étienne Bézier (1910-1999), Renault
Paul de Faget de Casteljau (*1930), Citroën
Сергeй Натaнович Бернштeйн (Sergei Bernstein) (1880-1968)
Paul de Faget de Casteljau (*1930), Citroën
Сергeй Натaнович Бернштeйн (Sergei Bernstein) (1880-1968)

Bézierova křivka n-tého stupně
- aproximační jednosegmentová křivka
- uniformní parametrizace
- řídící polygon křivky, konvexní obal
- lineární kombinace bodů řídícího polygonu
Rovnice Bézierovy křivky
řídící polygon $V_0, V_1,\dots,V_n$
$\Downarrow$
vektorová rovnice křivky
$$P(t)=\sum_{i=0}^{n}B_{i,n}(t)V_i,\ t\in[0,1]$$
kde $$B_{i,n}(t)=\binom{n}{i}t^i(1-t)^{n-i},\ i=0,1,\dots,n$$
jsou tzv. Bernsteinovy polynomy
jsou tzv. Bernsteinovy polynomy
Bernsteinovy polynomy
odvození 1
lineární kombinace bodů
$$P(t)=\sum_{i=0}^{n}B_{i,n}(t)V_i\ \ \text{je bod}\ \Leftrightarrow \sum_{i=0}^{n}B_{i,n}(t)=1$$
$$1=1^n=(1-t+t)^n=\sum_{i=0}^{n}\binom{n}{i}(1-t)^{n-i}t^i$$
$$B_{i,n}(t)=\binom{n}{i}t^i(1-t)^{n-i}$$
odvození 2
lineární interpolace
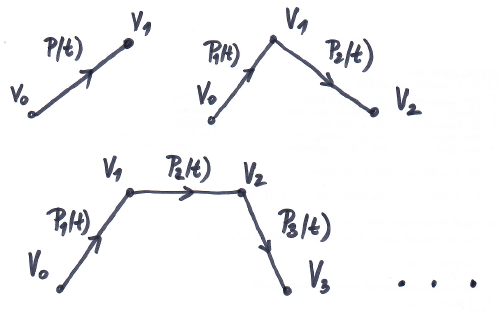
odvození 2
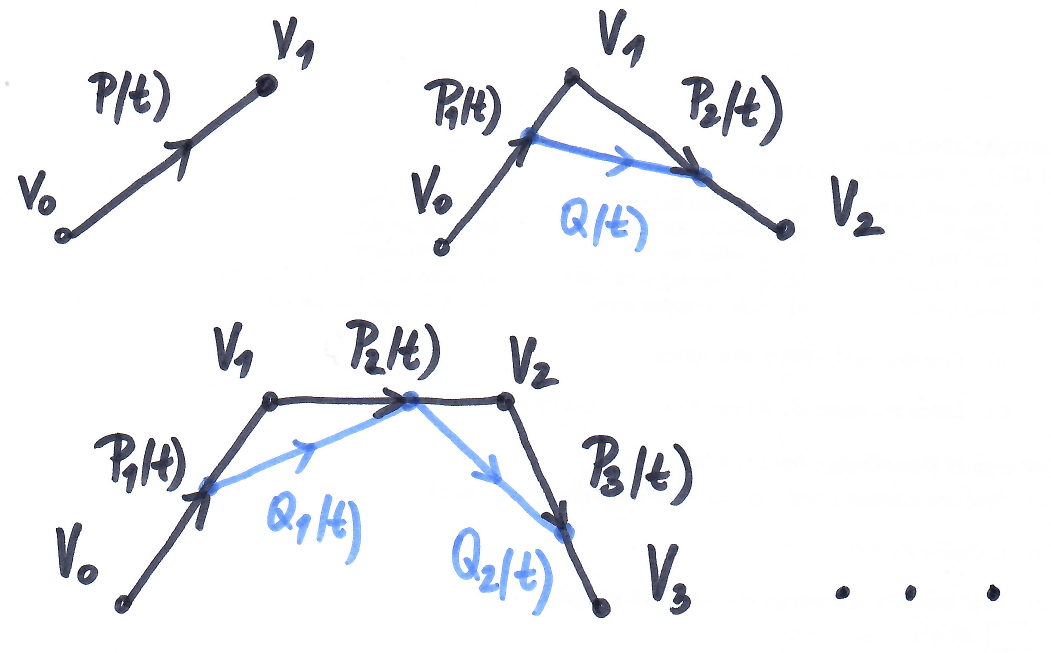
odvození 2

Bézierova křivka prvního stupně (lineární)
řídící polygon $V_0,V_1$
1) úsečka mezi dvěma řídicími body $V_0, V_1$
$$P(t)=V_0+t\vec{V_0V_1}=V_0+t(V_1-V_0),\ t\in[0,1]$$2) nebo vzorec
$$P(t)=B_{0,1}(t)V_0+B_{1,1}(t)V_1,\ t\in[0,1]$$
$B_{0,1}=\binom{1}{0}t^0(1-t)^{1-0}=1-t$
$B_{1,1}=\binom{1}{1}t^1(1-t)^{1-1}=t$
$B_{1,1}=\binom{1}{1}t^1(1-t)^{1-1}=t$
$$P(t)=(1-t)V_0+tV_1,\ t\in[0,1]$$
Bézierova křivka druhého stupně (kvadratická)
řídící body $V_0,V_1,V_2$
úsečka mezi $V_0,V_1$ $\Rightarrow P_1(t)=(1-t)V_0+ tV_1,\ t\in[0,1]$
úsečka mezi $V_1,V_2 \Rightarrow P_2(t)=(1-t)V_1+ tV_2,\ t\in[0,1]$
úsečka mezi $P_1(t),P_2(t) \Rightarrow Q(t)=(1-t)P_1(t)+ tP_2(t),\ t\in[0,1]$
$$Q(t)=(1-t)^2V_0+2t(1-t)V_1+t^2V_2,\ t\in[0,1]$$
tedy vzorec
$$Q(t)=B_{0,2}(t)V_0+B_{1,2}(t)V_1+B_{2,2}(t)V_2,\ t\in[0,1]$$
kde
$B_{0,2}=\binom{2}{0}t^0(1-t)^{2-0}=(1-t)^2$
$B_{1,2}=\binom{2}{1}t^1(1-t)^{2-1}=2t(1-t)$
$B_{2,2}=\binom{2}{2}t^2(1-t)^{2-2}=t^2$
$B_{1,2}=\binom{2}{1}t^1(1-t)^{2-1}=2t(1-t)$
$B_{2,2}=\binom{2}{2}t^2(1-t)^{2-2}=t^2$
Bézierova křivka třetího stupně (kubická)
řídící body $V_0,V_1,V_2,V_3$
postupně přes úsečky $\ldots\Rightarrow$ vzorec
$$P(t)=B_{0,3}(t)V_0+B_{1,3}(t)V_1+B_{2,3}(t)V_2+B_{3,3}(t)V_3,\ t\in[0,1]$$
kde
$B_{0,3}=\binom{3}{0}t^0(1-t)^{3-0}=(1-t)^3$
$B_{1,3}=\binom{3}{1}t^1(1-t)^{3-1}=3t(1-t)^2$
$B_{2,3}=\binom{3}{2}t^2(1-t)^{3-2}=3t^2(1-t)$
$B_{3,3}=\binom{3}{3}t^3(1-t)^{3-3}=t^3$
$B_{1,3}=\binom{3}{1}t^1(1-t)^{3-1}=3t(1-t)^2$
$B_{2,3}=\binom{3}{2}t^2(1-t)^{3-2}=3t^2(1-t)$
$B_{3,3}=\binom{3}{3}t^3(1-t)^{3-3}=t^3$
Vlastnosti Bézierových křivek
Bod křivky - počáteční a koncový
$$P(t)=\sum_{i=0}^{n}B_{i,n}(t)V_i,\ t\in[0,1]$$
počáteční bod křivky $\iff t=0$
koncový bod křivky $\iff t=1$
koncový bod křivky $\iff t=1$
Bernsteinovy polynomy - přehled
| $n$ | $1$ | $2$ | $3$ | $4$ | $\ldots$ |
|---|---|---|---|---|---|
| $B_{0,n}$ | $1-t$ | $(1-t)^2$ | $(1-t)^3$ | $(1-t)^4$ | $\ldots$ |
| $B_{1,n}$ | $t$ | $2t(1-t)$ | $3t(1-t)^2$ | $4t(1-t)^3$ | $\ldots$ |
| $B_{2,n}$ | $\times$ | $t^2$ | $3t^2(1-t)$ | $6t^2(1-t)^2$ | $\ldots$ |
| $B_{3,n}$ | $\times$ | $\times$ | $t^3$ | $4t^3(1-t)$ | $\ldots$ |
| $B_{4,n}$ | $\times$ | $\times$ | $\times$ | $t^4$ | $\ldots$ |
| $\ldots$ | $\times$ | $\times$ | $\times$ | $\times$ | $\ldots$ |
Bernsteinovy polynomy - průběhy

$\Rightarrow$ počáteční bod $P(0)=V_0$
$\Rightarrow$ koncový bod $P(1)=V_n$
$\Rightarrow$ koncový bod $P(1)=V_n$
Tečný vektor křivky - počáteční a koncový
$$P'(t)=\sum_{i=0}^{n}B_{i,n}'(t)V_i,\ t\in[0,1]$$
počáteční tečný vektor $\iff t=0$
koncový tečný vektor $\iff t=1$
koncový tečný vektor $\iff t=1$
lineární Bézierova křivka
| $i$ | $B_{i,1}(t)$ | $B_{i,1}'(t)$ | $B_{i,1}'(0)$ | $B_{i,1}'(1)$ |
|---|---|---|---|---|
| $0$ | $1-t$ | $-1$ | $-1$ | $-1$ |
| $1$ | $\phantom{1-}t$ | $\phantom{-}1$ | $\phantom{-}1$ | $\phantom{-}1$ |
$$P'(0)=-V_0+V_1=\vec{V_0V_1}$$ $$P'(1)=-V_0+V_1=\vec{V_0V_1}$$
kvadratická Bézierova křivka
| $i$ | $B_{i,2}(t)$ | $B_{i,2}'(t)$ | $B_{i,2}'(0)$ | $B_{i,2}'(1)$ |
|---|---|---|---|---|
| $0$ | $(1-t)^2$ | $-2(1-t)$ | $-2$ | $\phantom{-}0$ |
| $1$ | $2t(1-t)$ | $2(1-t)-2t$ | $\phantom{-}2$ | $-2$ |
| $2$ | $\phantom{-}t^2$ | $\phantom{-}2t$ | $\phantom{-}0$ | $\phantom{-}2$ |
$$P'(0)=-2V_0+2V_1=2\vec{V_0V_1}$$ $$P'(1)=-2V_1+2V_2=2\vec{V_1V_2}$$
kubická Bézierova křivka
| $i$ | $B_{i,3}(t)$ | $B_{i,3}'(t)$ | $B_{i,3}'(0)$ | $B_{i,3}'(1)$ |
|---|---|---|---|---|
| $0$ | $(1-t)^3$ | $-3(1-t)^2$ | $-3$ | $\phantom{-}0$ |
| $1$ | $3t(1-t)^2$ | $3(1-t)^2-6t(1-t)$ | $\phantom{-}3$ | $\phantom{-}0$ |
| $2$ | $3t^2(1-t)$ | $6t(1-t)-3t^2$ | $\phantom{-}0$ | $-3$ |
| $3$ | $\phantom{-}t^3$ | $\phantom{-}3t^2$ | $\phantom{-}0$ | $\phantom{-}3$ |
$$P'(0)=-3V_0+3V_1=3\vec{V_0V_1}$$ $$P'(1)=-3V_2+3V_3=3\vec{V_2V_3}$$
Bézierova křivka n-tého stupně
$P'(0)=n\vec{V_0V_1}$
$P'(1)=n\vec{V_{n-1}V_{n}}$
$P(0)=V_1$
$P(1)=V_n$
$P'(1)=n\vec{V_{n-1}V_{n}}$
$P(0)=V_1$
$P(1)=V_n$
de Casteljau algoritmus
de Casteljau algoritmus
lineární křivka
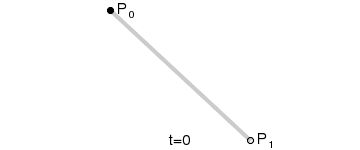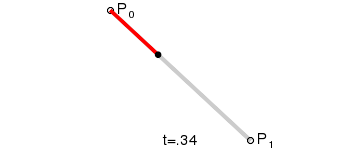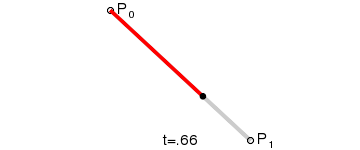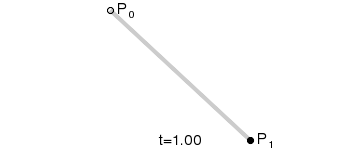
de Casteljau algoritmus
kvadratická křivka
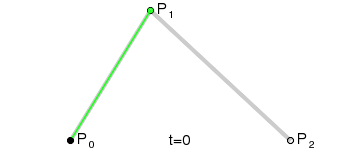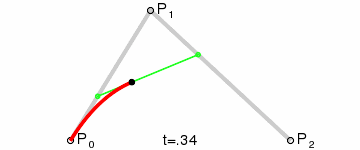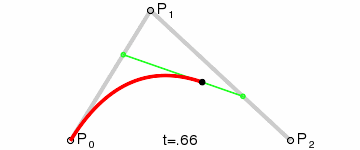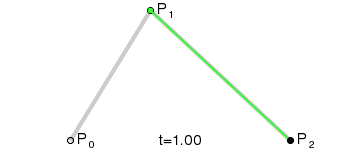
de Casteljau algoritmus
kubická křivka

de Casteljau algoritmus
křivka 4. stupně
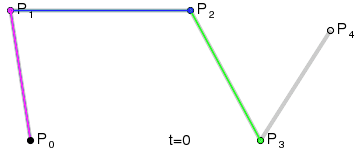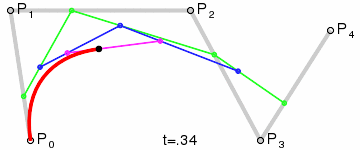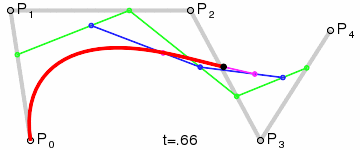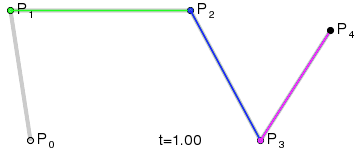
de Casteljau algoritmus

$$P'(t_0)=n\vec{MN}$$
Napojování křivek
- spojitost geometrická - $G^n$
- spojitost parametrická - $C^n$
Geometrická spojitost napojení 2 křivek
$G^0 \iff$ společný bod
$G^1 \iff G^0 + $stejná tečna ve společném bodě
$G^2 \iff G^1 +$ stejná křivost ve společném bodě
$G^1 \iff G^0 + $stejná tečna ve společném bodě
$G^2 \iff G^1 +$ stejná křivost ve společném bodě

Parametrická spojitost napojení 2 křivek
Pro dvě uniformní křivky $P(t)$ a $Q(s)$:
$C^0 \iff P(1)=Q(0)$
$C^1 \iff C^0 \land P'(1)=Q'(0)$
$C^2 \iff C^1 \land P''(1)=Q''(0)$
...
$C^1 \iff C^0 \land P'(1)=Q'(0)$
$C^2 \iff C^1 \land P''(1)=Q''(0)$
...
spojitost parametrická $\Rightarrow$ spojitost geometrická