Počítačová grafika 2023/24

Plochy

Plocha

každá souvislá podmnožina $\mathbb{E}_3$, která je spojitým obrazem souvislé oblasti $I\subset \mathbb{E}_2$.

  • vektorová rovnice plochy
    $$P(u,v)=(x(u,v),y(u,v),z(u,v)),\ (u,v)\in I$$
  • plát $\iff I=[a,b]\times[c,d]$
  • plát s uniformní parametrizací $\iff I=[0,1]^2$

Plát

  • parametrické (křivočaré) souřadnice $(u_0,v_0)$ bodu plochy $P(u_0,v_0)$
  • parametrická u-křivka plochy $P(u,v_0)=(x(u,v_0),y(u,v_0),z(u,v_0))=P_{v_0}(u), u\in[a,b]$
  • parametrická v-křivka plochy $P(u_0,v)=P_{u_0}(v), v\in [c,d]$

Plát s uniformní parametrizací

  • rohy plátu $P_{0,0}=P(0,0),P_{0,1}=P(0,1),P_{1,0}=P(1,0),P_{1,1}=P(1,1)$
  • okrajové křivky plátu $P_0(u),P_1(u),P_0(v),P_1(v)$

Plocha

tečné vektory \[P^u(u,v)= \frac{\partial P(u,v)}{\partial u}=\bigg(\frac{\partial x(u,v)}{\partial u},\frac{\partial y(u,v)}{\partial u},\frac{\partial z(u,v)}{\partial u}\bigg)\] \[P^v(u,v)= \frac{\partial P(u,v)}{\partial v}=\bigg(\frac{\partial x(u,v)}{\partial v},\frac{\partial y(u,v)}{\partial v},\frac{\partial z(u,v)}{\partial v}\bigg)\]

tečná rovina a normála

\[\vec{n}(u,v)=P^u(u,v)\times P^v(u,v)\]

vektor zkrutu \[P^{uv}(u,v)=\frac{\partial^2 P(u,v)}{\partial u\partial v}=\frac{\partial^2 P(u,v)}{\partial v\partial u}\]

Bézierova plocha

Bézierova plocha

aproximační plocha

Dáno: mapa plátu

$$M=\begin{pmatrix}V_{00}&V_{01}&\dots&V_{0n}\\V_{10}&V_{11}&\dots&V_{1n}\\ \vdots&\vdots& &\vdots\\V_{m0}&V_{m1}&\dots&V_{mn}\end{pmatrix}$$
$(m+1)\times(n+1)$ bodů

Bézierova plocha

síť řídících bodů, mapa plátu

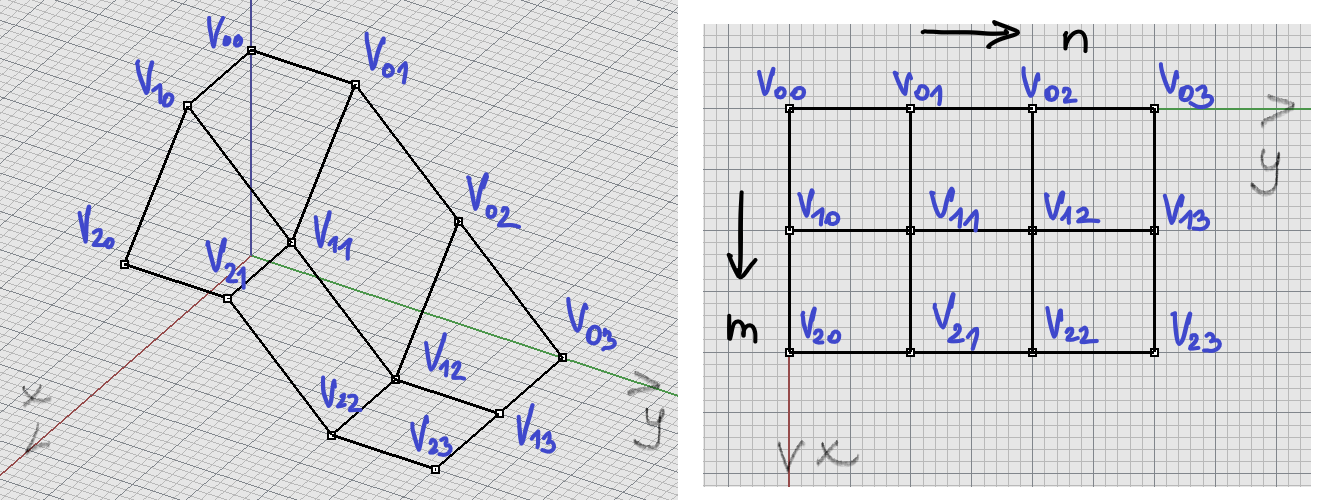
Bézierova plocha

Vektorová rovnice:

$$P(u,v)=\mathscr{B}(u)\cdot M\cdot {\mathscr{B}(v)}^T;\ (u,v)\in [0,1]^2$$
kde

$\mathscr{B}(u)=(B_{0m}(u),B_{1m}(u),\dots,B_{mm}(u))\\ \mathscr{B}(v)=(B_{0n}(v),B_{1n}(v),\dots,B_{nn}(v))$

jsou Bernsteinovy polynomy

Bézierova plocha - příklad

Je dána mapa M plátu:

$$M=\begin{pmatrix}(0,0,2)&(0,1,1)&(0,2,1)&(0,3,0)\\(1,0,2)&(1,1,1)&(1,2,0)&(1,3,0)\\(2,0,1)&(2,1,1)&(2,2,0)&(2,3,0)\end{pmatrix}.$$
    Určete:
  • vektorovou rovnici plátu
  • rovnice tečných vektorů parametrických křivek
  • rovnici vektorů zkrutu
Načrtněte okrajové křivky plátu.
vektorová rovnice plátu:

$$P(u,v)=\mathscr{B}(u)\cdot\begin{pmatrix}(0,0,2)&(0,1,1)&(0,2,1)&(0,3,0)\\(1,0,2)&(1,1,1)&(1,2,0)&(1,3,0)\\(2,0,1)&(2,1,1)&(2,2,0)&(2,3,0)\end{pmatrix}\cdot{\mathscr{B}(v)^T}$$
kde $\mathscr{B}(u)$ a $\mathscr{B}(v)$ obsahují Bernsteinovy polynomy příslušného stupně

$$\Downarrow$$
$$\mathscr{B}(u)=(B_{02}(u),B_{12}(u),B_{22}(u))\\ \mathscr{B}(v)=(B_{03}(v),B_{13}(v),B_{23}(v),B_{33}(v))$$
Stupně Bernsteinových polynomů souvisí s maticí řídicích bodů (zde typ 3x4) a je od nich odvozen i název konkrétní plochy - v tomto případě Bézierova kvadraticko-kubická plocha
vektorová rovnice plátu:

$$P(u,v)=(2u,3v,-2u^2v^3+6uv^3+3u^2v-6uv^2-2v^3-u^2+3v^2-3v+2);\ (u,v)\in[0,1]^2$$
rovnice tečných vektorů parametrických křivek:

$P^u(u,v)=(2,0,-4uv^3+6v^3+6uv-6v^2-2u)\\P^v(u,v)=(0,3,-6u^2v^2+18uv^2+3u^2-12uv-6v^2+6v-3)$

rovnice vektorů zkrutu:

$P^{uv}(u,v)=(0,0,-12uv^2+18v^2+6u-12v)$
tečné vektory v rohových bodech:

$$\begin{matrix}P^u(0,0)=(2,0,0)&P^v(0,0)=(0,3,-3)\\P^u(0,1)=(2,0,0)&P^v(0,1)=(0,3,-3)\\P^u(1,0)=(2,0,-2)&P^v(1,0)=(0,3,0)\\P^u(1,1)=(2,0,0)&P^v(1,1)=(0,3,0)\end{matrix}$$
vektory zkrutu v rohových bodech:

$$P^{uv}(0,0)=(0,0,0)=P^{uv}(1,1)\\P^{uv}(0,1)=(0,0,6)=P^{uv}(1,0)$$
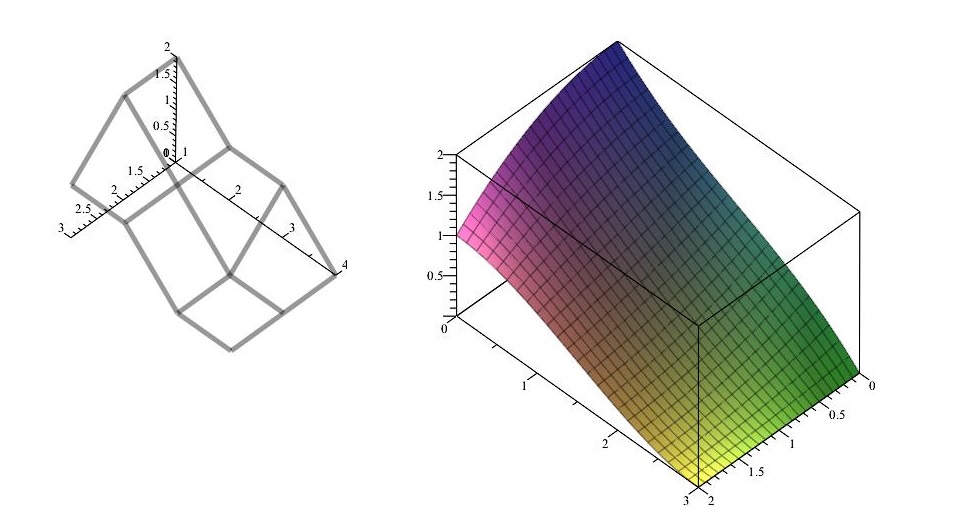
síť řídících bodů + plocha (Maple)
síť řídících bodů a okrajové křivky (Rhino)

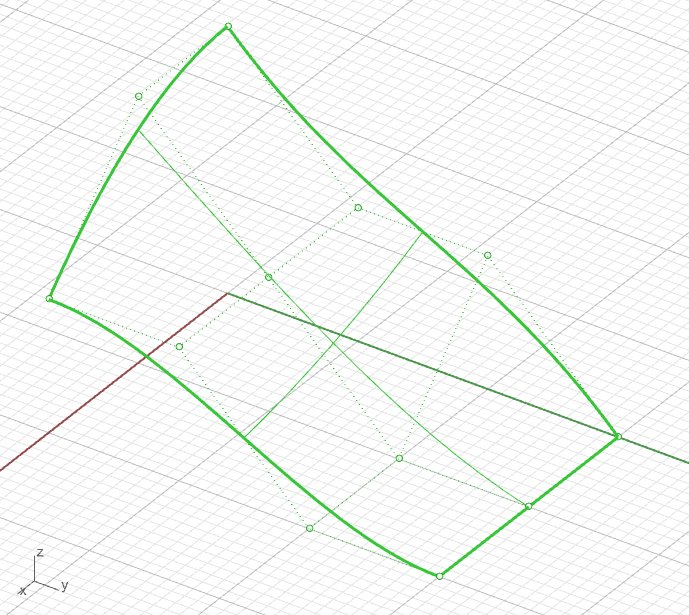
Bézierova plocha - vlastnosti

  • interpoluje rohy řídící sítě
  • okraje plátu jsou Bézierovy křivky
  • tečné vektory v rozích plátu jsou násobky krajních ramen řídících polygonů okrajových křivek
  • vektor zkrutu v rohu plátu je určen řídícími body rohového oka sítě
  • jestliže je rohové oko sítě rovnoběžník, je vektor zkrutu nulový

Plátování

Plátování

Uvažujme dva pláty $P(u,v);(u,v)\in[0,1]^2$ a $R(\bar{u},\bar{v});(\bar{u},\bar{v})\in[0,1]^2$.

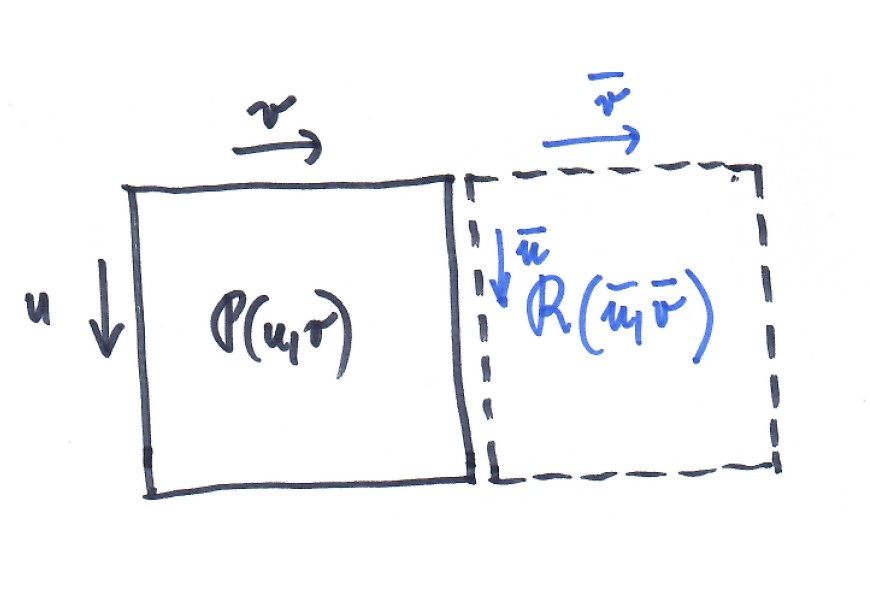
Plátování

spojitost plátů je definována pomocí spojitosti napojení podél okrajové křivky

$C^0$ spojitost $\Leftrightarrow$ společná okrajová křivka

$C^1$ spojitost $\Leftrightarrow$ $C^0$ + stejné příčné tečné vektory v bodech společné okrajové křivky

$C^2$ spojitost $\Leftrightarrow$ $C^1$ + stejné příčné vektory druhých derivací v bodech společné okrajové křivky
$C^3$ spojitost ...

Plátování Bézierových ploch

tady řešeno pouze napojení plátů stejného stupně!

\[ M_P= \begin{pmatrix} V_{0,0} & \cdots & V_{0,n} \\ \vdots & ~ & \vdots \\ V_{m,0} & \cdots & V_{m,n} \end{pmatrix}, M_R= \begin{pmatrix} U_{0,0} & \cdots & U_{0,n} \\ \vdots & ~ & \vdots \\ U_{m,0} & \cdots & U_{m,n} \end{pmatrix} \]

Plátování Bézierových ploch

$C^n$ spojité napojení $(n=0,1,2,\dots)$ podél u-okraje
$\Downarrow \Uparrow$
stejný sloupec + po řádcích splněny podmínky $C^n$ spojitosti Bezierových v-křivek

$C^n$ spojité napojení $(n=0,1,2,\dots)$ podél v-okraje
$\Downarrow \Uparrow$
stejný řádek + po sloupcích splněny podmínky $C^n$ spojitosti Bezierových u-křivek

Příklad

Bézierova plocha $P$ je dána mapou
\[ M_P = \begin{pmatrix} (0,0,2)&(0,1,1)&(0,2,1)&(0,3,0)\\ (1,0,2)&(1,1,1)&(1,2,0)&(1,3,0)\\ (2,0,1)&(2,1,1)&(2,2,0)&(2,3,0) \end{pmatrix}.\]
Určete mapu $M_R$ Bézierovy plochy $R$, která je napojena k ploše $P$ podél okraje $P_0(u)$ se spojitostí $C^0$.
Určete mapu $M_S$ Bézierovy plochy $S$, která je napojena k ploše $P$ podél okraje $P_1(v)$ se spojitostí $C^1$.
Určete mapu $M_T$ Bézierovy plochy $T$, která je napojena k ploše $P$ podél okraje $P_1(u)$ se spojitostí $C^2$.
Všechny plochy jsou stejného typu, z-ové souřadnice bodů, které neovlivní danou spojitost volte nulové.
Plát P:
Plát R napojený podél $P_0(u)$ okraje, spojitost $C^0$:

\[ \begin{matrix} (0,-3,0)&(0,-2,0)&(0,-1,0)&(0,0,2)&\mid &(0,0,2) & \cdots & (0,3,0) \\ (1,-3,0) & (1,-2,0) & (1,-1,0) & (1,0,2)&\mid&(1,0,2) & ~ & \vdots \\ (2,-3,0) & (2,-2,0) & (2,-1,0) & (2,0,1)&\mid&(2,0,1) & ~\cdots & (2,3,0) \end{matrix}\]
Mapa plátu $R$

\[ M_R= \begin{pmatrix} (0,-3,0)&(0,-2,0)&(0,-1,0)&(0,0,2) \\ (1,-3,0) & (1,-2,0) & (1,-1,0) & (1,0,2) \\ (2,-3,0) & (2,-2,0) & (2,-1,0) & (2,0,1) \end{pmatrix}\]
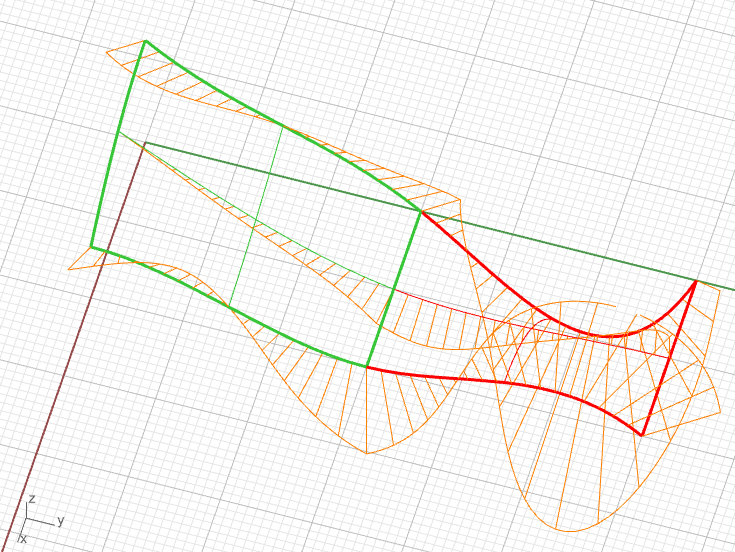
Plát R napojený podél $P_0(u)$ okraje, spojitost $C^0$ - zebra
Plát R napojený podél $P_0(u)$ okraje, spojitost $C^0$ - grafy křivosti
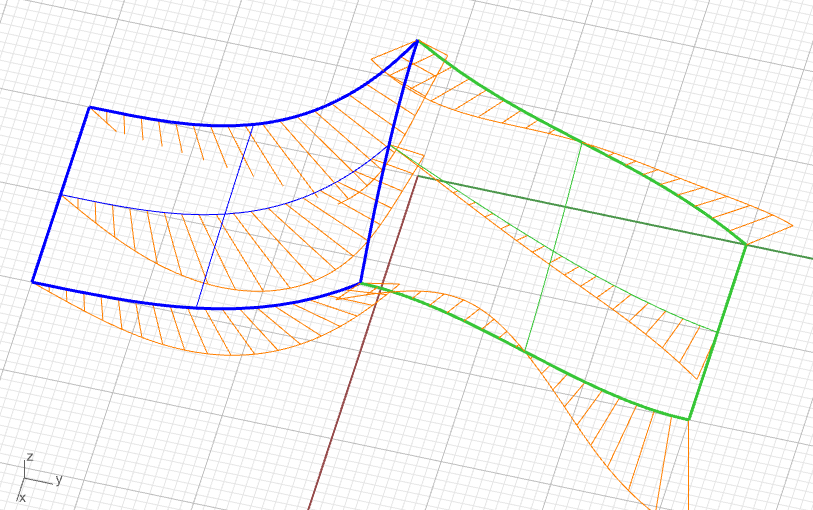
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$

\[ \begin{matrix} (0,0,2) & (0,1,1) & (0,2,1) & (0,3,0) \\ (1,0,2) & (1,1,1) & (1,2,0) & (1,3,0) \\ (2,0,1) & (2,1,1) & (2,2,0) & (2,3,0) \\ --- & --- & --- & --- \\ (2,0,1) & (2,1,1) & (2,2,0) & (2,3,0)\\ (3,0,0)&(3,1,1)&(3,2,0)&(3,3,0)\\ (4,0,0)&(4,1,0)&(4,2,0)&(4,3,0) \end{matrix}\]
Mapa plátu $S$:

\[ M_S= \begin{pmatrix} (2,0,1) & (2,1,1) & (2,2,0) & (2,3,0)\\ (3,0,0)&(3,1,1)&(3,2,0)&(3,3,0)\\ (4,0,0)&(4,1,0)&(4,2,0)&(4,3,0) \end{pmatrix}\]
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$ - zebra
Plát S napojený podél $P_1(v)$ okraje, spojitost $C^1$ - grafy křivosti
Plát T napojený podél $P_1(u)$ okraje, spojitost $C^2$:

\[ \begin{matrix} (0,0,2) & (0,1,1) & (0,2,1) & (0,3,0)&\mid & (0,3,0) & (0,4,-1) & (0,5,-3) & (0,6,0) \\ (1,0,2) & (1,1,1) & (1,2,0) & (1,3,0)&\mid & (1,3,0) & (1,4,0) & (1,5,1) & (1,6,0)\\ (2,0,1) & (2,1,1) & (2,2,0) & (2,3,0) &\mid & (2,3,0) & (2,4,0) & (2,5,1) & (2,6,0) \end{matrix}\]
Mapa plátu $T$

\[ M_T= \begin{pmatrix} (0,3,0) & (0,4,-1) & (0,5,-3) & (0,6,0) \\ (1,3,0) & (1,4,0) & (1,5,1) & (1,6,0) \\ (2,3,0) & (2,4,0) & (2,5,1) & (2,6,0) \end{pmatrix}\]
Plát T napojený podél $P_1(u)$ okraje, spojitost $C^2$ - zebra
Plát T napojený podél $P_1(u)$ okraje, spojitost $C^2$ - grafy křivosti

Příště: Ukotvená plocha