Počítačová grafika 2023/24
Plochy
Uniformní Ukotvená Bikubická
B-spline plocha
- aproximační plocha - segmentovaná
- dána sítí řídících bodů (minimálně 4x4)
- okraje jsou ukotvené kubiky
- jednotlivé segmenty jsou Bézierovy bikubické pláty (řídící body z konstrukce segmentů řádkových a sloupcových ukotvených kubik)
- všechny segmenty jsou na sebe napojeny s $C^2$ spojitostí
- zobecněním těchto ploch jsou NeUniformní Racionální B-Spline plochy (NURBS)
Uniformní Ukotvená Bikubická
B-spline plocha

Příklad
Je dán Bézierův bikubický plát $P(u,v)$ mapou $M_P$. Určete mapu $M_R$ dalšího Bézierova bikubického plátu $R(s,t)$, který bude napojen na $P(u,v)$ podél křivky $P_1(u)$ se spojitostí $C^2$ (u bodů neovlivňujících spojitost volte z-souřadnici nulovou). Určete také řídicí body (= mapu plátu $M_T$) ukotvené bikubické (B-spline) plochy $T$, která je tvořena segmenty $P$ a $R$.
\[ M_P= \begin{pmatrix} (0,0,3) & (0,1,0) & (0,2,3) & (0,3,1) \\ (1,0,2) & (1,1,1) & (1,2,2) & (1,3,1) \\ (2,0,4) & (2,1,1) & (2,2,1) & (2,3,0) \\ (3,0,0) & (3,1,0) & (3,2,0) & (3,3,0) \end{pmatrix} \]
Podle podmínek $\color{blue}{C^0},\color{green}{C^1}$ a $\color{red}{C^2}$ spojitosti řádkových Bézierových kubik doplnit z-souřadnice plátu $R$
\[M_{P_z}|M_{R_z}=\begin{pmatrix} 3 & 0 & 3 & 1 & | & \color{blue}{1} & \color{green}{-1} & \color{red}{-8} & 0 \\ 2 & 1 & 2 & 1 & | & \color{blue}{1} & \color{green}{0} & \color{red}{-3} & 0 \\ 4 & 1 & 1 & 0 & | & \color{blue}{0} & \color{green}{-1} & \color{red}{-3} & 0 \\ 0 & 0 & 0 & 0 & | & \color{blue}{0} & \color{green}{0} & \color{red}{0} & 0 \\ \end{pmatrix} \]
Mapa plátu $R$
\[ M_R= \begin{pmatrix} (0,3,1) & (0,4,-1) & (0,5,-8) & (0,6,0) \\ (1,3,1) & (1,4,0) & (1,5,-3) & (1,6,0) \\ (2,3,0) & (2,4,-1) & (2,5,-3) & (2,6,0) \\ (3,3,0) & (3,4,0) & (3,5,0) & (3,6,0) \end{pmatrix} \]
Konstrukce bodů mapy $M_R$

Kontrola napojení plátů $P$ a $R$ zebřími pruhy

Místo společného uzlu každé řádkové ukotvené kubiky doplnit její řídicí bod (= spojit dvě Bézierovy kubiky do jedné ukotvené kubiky) a odstranit z každé kubiky jeden další bod (pro ukotvenou není řídicí, leží v polovině ramene)
\[ \begin{matrix} (0,0,3) & (0,1,0) & \color{blue}{(0,2,3)} & \color{red}{(0,3,1)} & | & \color{red}{(0,3,1)} & \color{blue}{(0,4,-1)} & (0,5,-8) & (0,6,0) \end{matrix} \]
\[\Downarrow\]
\[ \begin{matrix} (0,0,3) & (0,1,0) & \boldsymbol{\color{red}{(0,3,6)}} & (0,5,-8) & (0,6,0) \end{matrix} \]
Konstrukce bodů mapy $M_T$ ukotvené plochy
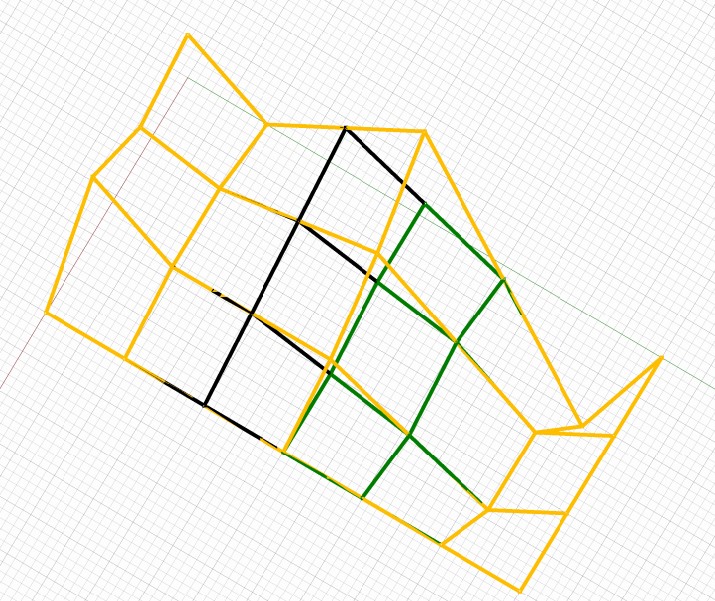
Mapa ukotvené bikubické plochy
\[ M_T= \begin{pmatrix} (0,0,3) & (0,1,0) & \color{red}{(0,3,6)} & (0,5,-8) & (0,6,0) \\ (1,0,2) & (1,1,1) & \color{red}{(1,3,3)} & (1,5,-3) & (1,6,0) \\ (2,0,4) & (2,1,1) & \color{red}{(2,3,1)} & (2,5,-3) & (2,6,0) \\ (3,0,0) & (3,1,0) & \color{red}{(3,3,0)} & (3,5,0) & (3,6,0) \end{pmatrix} \]
Ukotvená plocha $T$

Pláty Bézierových ploch a ukotvená plocha $T$

Příklad
Určete řídicí body jednotlivých plátů Bézierových bikubických ploch, ze kterých je složena ukotvená bikubická B-spline plocha daná mapou M,
\[ M= \begin{pmatrix} (0,0,0) & (0,10,0) & (0,20,0) & (0,30,0) & (0,40,0) \\ (10,0,0) & (10,10,5) & (10,20,5) & (10,30,25) & (10,40,0)\\ (20,0,0) & (20,10,-5) & (20,20,-5) & (20,30,15) & (20,40,0) \\ (30,0,0) & (30,10,25) & (30,20,-15) & (30,30,45) & (30,40,0) \\ (40,0,0) & (40,10,0) & (40,20,0) & (40,30,0) & (40,40,0) \end{pmatrix} \]
Řídicí síť ukotvené plochy
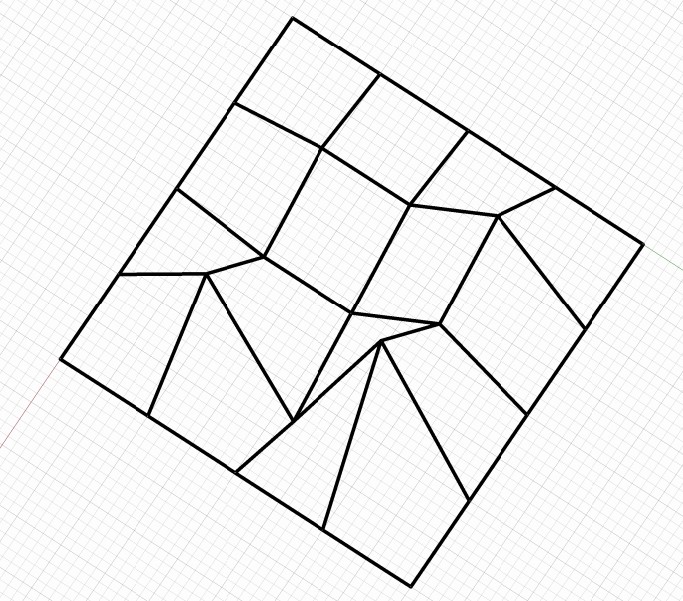
Ukotvená plocha
Po řádcích doplnit řídicí body segmentů (jsou to Bézierovy kubiky) ukotvených kubik
viz. například druhý řádek
viz. například druhý řádek
\[ \begin{matrix} (10,0,0) & (10,10,5) & (10,20,5) & (10,30,25) & (10,40,0) \end{matrix} \]
\[\Downarrow \]
\[ \begin{matrix} (10,0,0) & (10,10,5) & \color{blue}{(10,15,5)} & \color{red}{(10,20,10)} & \color{blue}{(10,25,15)} & (10,30,25) & (10,40,0) \end{matrix} \]
Konstrukce řídicích bodů "řádkových" segmentů
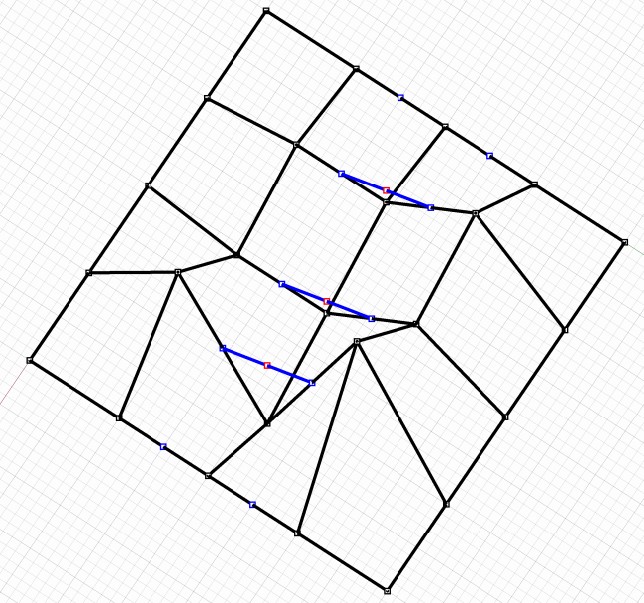
Nová "mapa" plátu je nyní typu 5x7
$\tilde{M}= \begin{pmatrix} (0,0,0) & (0,10,0) & \color{blue}{(0,15,0)} & \color{red}{(0,20,0)} & \color{blue}{(0,25,0)} & (0,30,0) & (0,40,0) \\ (10,0,0) & (10,10,5) & \color{blue}{(10,15,5)} & \color{red}{(10,20,10)} & \color{blue}{(10,25,15)} & (10,30,25) & (10,40,0) \\ (20,0,0) & (20,10,-5) & \color{blue}{(20,15,-5)} & \color{red}{(20,20,0)} & \color{blue}{(20,25,5)} & (20,30,15) & (20,40,0) \\ (30,0,0) & (30,10,25) & \color{blue}{(30,15,5)} & \color{red}{(30,20,10)} & \color{blue}{(30,25,15)} & (30,30,45) & (30,40,0) \\ (40,0,0) & (40,10,0) & \color{blue}{(40,15,0)} & \color{red}{(40,20,0)} & \color{blue}{(40,25,0)} & (40,30,0) & (40,40,0) \end{pmatrix} $
Stejnou konstrukci nyní provést i pro sloupcové ukotvené kubiky $\rightarrow$ matice 7x7

Konstrukce řídicích bodů "sloupcových" segmentů
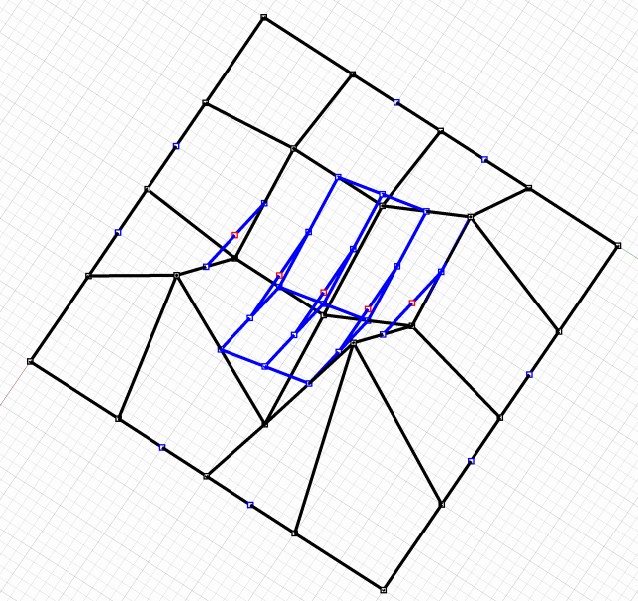

"Rohové" matice 4x4 vybrané z matice $\bar{M}$ jsou mapy plátů jednotlivých Bézierových bikubických ploch, které jsou na sebe napojené s $C^2$ spojitostí a tvoří segmenty původní ukotvené bikubické B-spline plochy.
"Mapa" napojených plátů Bézierových bikubických ploch

Pláty Bézierových bikubických ploch
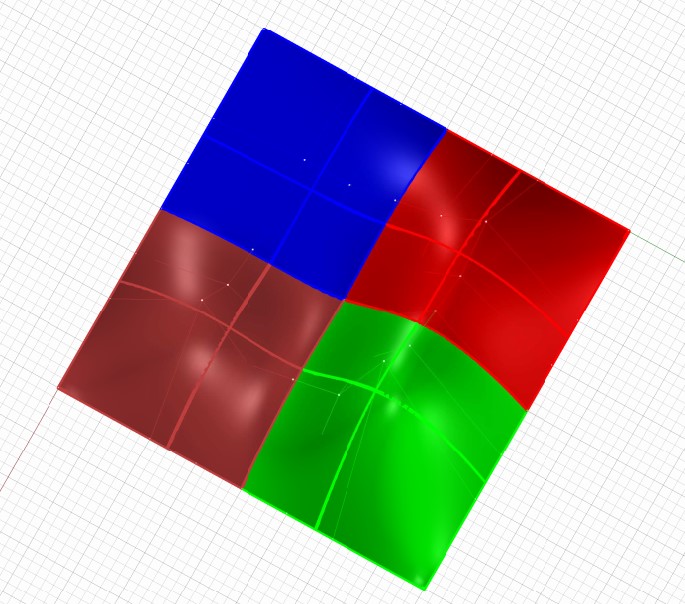
Kontrola spojitosti plátů a srovnání s ukotvenou plochou

Coonsova bilineární plocha
interpolační plocha
Dáno: okrajové křivky $P_0(u), P_1(u), P_0(v), P_1(v)$
- tzv. křivočarý čtyřúhelník
- tzv. křivočarý čtyřúhelník

Coonsova bilineární plocha
Vektorová rovnice:$$P(u,v)=(1-u,1,u)\cdot M\cdot\begin{pmatrix}1-v\\1\\v\end{pmatrix};\ (u,v)\in [0,1]^2$$
Mapa plátu:$$M=\begin{pmatrix}-P_{00}&P_0(v)&-P_{01}\\P_0(u)&\vec{o}&P_1(u)\\-P_{10}&P_1(v)&-P_{11}\end{pmatrix}$$
Coonsova bilineární plocha
Mapa plátu:

Coonsova bilineární plocha

Coonsova bilineární plocha - vlastnosti
- interpoluje dané 4 okraje
- interpoluje rohy plátu
Vztahy mezi plochami
Coonsova bilineární $\to$ Bézierova
Coonsova bilineární plocha
mapa plátu
\[ M = \begin{pmatrix} -P_{0,0} & P_{0}(v) & -P_{0,1} \\ P_{0}(u) & \vec{0} & P_{1}(u) \\ -P_{1,0} & P_{1}(v) & -P_{1,1} \\ \end{pmatrix} \]
Coonsova bilineární plocha
speciálně: okrajové křivky - Bézierovy kubiky
\[ \begin{matrix} ~ & ~ & ~ & ~ & P_{0}(v) & ~ & ~ & ~ & ~ \\ ~ & V_{0,0} & \to & V_{0,1} & \to & V_{0,2} & \to & V_{0,3} & ~ \\ ~ & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & \\ ~ & V_{1,0} & ~ & ~ & ~ & ~ & ~ & V_{1,3} & \\ P_{0}(u) & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & P_{1}(u)\\ ~ & V_{2,0} & ~ & ~ & ~ & ~ & ~ & V_{2,3} & \\ ~ & \downarrow & ~ & ~ & ~ & ~ & ~ & \downarrow & \\ ~ & V_{3,0} & \to & V_{3,1} & \to & V_{3,2} & \to & V_{3,3} & ~ \\ ~ & ~ & ~ & ~ & P_{1}(v) & ~ & ~ & ~ & ~ \\ \end{matrix} \]
Coonsova bilineární plocha
okrajové křivky - Bézierovy kubiky
\[ M = \begin{pmatrix} -V_{0,0} & P_{0}(v) & -V_{0,3} \\ P_{0}(u) & \vec{0} & P_{1}(u) \\ -V_{3,0} & P_{1}(v) & -V_{3,3} \\ \end{pmatrix} \]
Coonsova bilineární plocha
$\downarrow $
Bézierova bikubická plocha
?
Bézierova plocha
mapa plátu
\[ M = \begin{pmatrix} V_{0,0} & V_{0,1} & V_{0,2} & V_{0,3} \\ V_{1,0} & ? & ? & V_{1,3} \\ V_{2,0} & ? & ? & V_{2,3} \\ V_{3,0} & V_{3,1} & V_{3,2} & V_{3,3} \end{pmatrix} \]
Coonsova bilineární $\to$ Bézierova
Postup - teorie:
- vektory zkrutu Coonsovy bilineární plochy získat výpočtem (konkrétní vektor v každém rohu)
- vyjádřit vektory zkrutu v rozích Bézierovy plochy (obecně, ve vyjádřeních figurují vnitřní body sítě)
- porovnat dva zkruty (Coons = Bézier) v každém rohu
- z rovnic vyjádřit neznámé vnitřní body sítě
Coonsova bilineární $\to$ Bézierova bikubická
Postup - praxe:
- vektory zkrutu Coonsovy bilineární plochy (rohy): \[P^{uv}(0,0), P^{uv}(0,1), P^{uv}(1,0), P^{uv}(1,1)\]
- vektory zkrutu Bézierovy plochy (obecně) \[ P^{uv}(u,v)=\mathscr{B}^{\prime}(u)\cdot M \cdot \mathscr{B}^{\prime}(v) \] kde \[\mathscr{B}^{\prime}(u) = (B_{03}^{\prime}(u),B_{13}^{\prime}(u),B_{23}^{\prime}(u),B_{33}^{\prime}(u))\] \[\mathscr{B}^{\prime}(v) = (B_{03}^{\prime}(v),B_{13}^{\prime}(v),B_{23}^{\prime}(v),B_{33}^{\prime}(v))^T\]
- konkrétně v rozích \[ \mathscr{B}^{\prime}(0)=(-3,3,0,0), \mathscr{B}^{\prime}(1)=(0,0,-3,3)\]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{0,0}$
- vektor zkrutu Bézierovy plochy: \[ P^{uv}(0,0)=(-3,3,0,0)\cdot M \cdot (-3,3,0,0)^T \] \[\Downarrow\] \[P^{uv}(0,0)=9V_{0,0}-9V_{1,0}-9V_{0,1}+9V_{1,1}\] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) - V_{0,0}+V_{1,0}+V_{0,1} \] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) - V_{0,0}+V_{1,0}+V_{0,1} + (V_{0,0}-V_{0,0})\] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \vec{V_{0,0}V_{1,0}} + \vec{V_{0,0}V_{0,1}} \]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{0,0}$
- pomocí vektoru zkrutu a tečných vektorů Coonsovy bilineární plochy: \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \vec{V_{0,0}V_{1,0}} + \vec{V_{0,0}V_{0,1}} \] \[\Downarrow\] \[V_{1,1}= \frac{1}{9}P^{uv}(0,0) + V_{0,0} + \frac{1}{3}P^{u}(0,0) + \frac{1}{3}P^{v}(0,0)\]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{1,0}$
- vektor zkrutu Bézierovy plochy: \[ P^{uv}(1,0)=(0,0,-3,3)\cdot M \cdot (-3,3,0,0)^T \] \[\Downarrow\] \[P^{uv}(1,0)=9V_{2,0}-9V_{3,0}-9V_{2,1}+9V_{3,1}\] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) - V_{3,0}+V_{2,0}+V_{3,1} \] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) - V_{3,0}+V_{2,0}+V_{3,1} + (V_{3,0}-V_{3,0})\] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} + \vec{V_{3,0}V_{2,0}} + \vec{V_{3,0}V_{3,1}} \]
Coonsova bilineární $\to$ Bézierova bikubická
Roh $P_{1,0}$
- pomocí vektoru zkrutu a tečných vektorů Coonsovy bilineární plochy: \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} + \vec{V_{3,0}V_{2,0}} + \vec{V_{3,0}V_{3,1}} \] \[\Downarrow\] \[V_{2,1}= -\frac{1}{9}P^{uv}(1,0) + V_{3,0} - \frac{1}{3}P^{u}(1,0) + \frac{1}{3}P^{v}(1,0)\]
Coonsova bilineární $\to$ Bézierova bikubická
Podobně ve zbylých rozích:
\[V_{1,1}= V_{0,0} + \frac{1}{3}P^{u}(0,0) + \frac{1}{3}P^{v}(0,0) + \frac{1}{9}P^{uv}(0,0)\]
\[V_{2,1}= V_{3,0} - \frac{1}{3}P^{u}(1,0) + \frac{1}{3}P^{v}(1,0) - \frac{1}{9}P^{uv}(1,0)\]
\[V_{1,2}= V_{0,3} + \frac{1}{3}P^{u}(0,1) - \frac{1}{3}P^{v}(0,1) - \frac{1}{9}P^{uv}(0,1)\]
\[V_{2,2}= V_{3,3} - \frac{1}{3}P^{u}(1,1) - \frac{1}{3}P^{v}(1,1) + \frac{1}{9}P^{uv}(1,1)\]
Coonsova bilineární $\to$ Bézierova bikubická
Pomocné schema pro určení znamének:
