Postup s vytvořenými skripty ze cvičení:

Popisuji matematický model inverzního kyvadla, odvozený metodou Lagrangeových rovnic II. druhu na cvičení. V souboru main.m upravíme část se vstupními parametry aby zahrnovaly všechny potřebné pro Vaši úlohu:

% parametry systemu
L = 0.02; % L [m]
parametry{1} = 0.1; % m [kg]
parametry{2} = 0.3; % M [kg]
parametry{3} = L; % L [m]
parametry{4} = 9.81; % g [m/s^2]
parametry{5} = 3; % b [N.s/m]
parametry{6} = 1e-3; % Is [kg.m^2]

Dále upravíme funkci DynSystem.m tak, že načteme parametry, sestavím matici M a vektor pravých stran Q a sestavíme derivaci stavů. Upravovaná část kódu:

m = parametry{1};
M = parametry{2};
L = parametry{3};
g = parametry{4};
b = parametry{5};
Is = parametry{6};

x = z(1);
phi = z(2);
dx = zt(1);
dphi = zt(2);

MaticeM = [M+m          m*L*cos(phi)
           m*L*cos(phi) m*L^2+Is];
VektorQ = [m*L*sin(phi)*dphi^2-b*dx + Vstupy(1)
           m*g*L*sin(phi)];

ztt = MaticeM\VektorQ;
dStavy = [dx;ztt(1);dphi;ztt(2)];

Poté nastavíme v main.m počáteční podmínky simulace (nejlépe ne rovnovážné, protože nejprve použijeme nulový vstup):

% pocatecni poloha
X0=[0;0;pi/8;0]; % [x,dx,phi,dphi]

A můžeme spustit simulaci, kód v souboru main.m:

% simulace
[t,x]=ode45(@(t,x) DynSystem(t,x,0,parametry),0:1e-5:10,X0);

Další část souboru main.m ukazuje vykreslení stavů a animaci pohybu.

Linearizuji soustavu pomocí Taylorova rozvoje a dosadím rovnovážný bod, můžu použít postup v DynSystem2lin.m, kde nejprve vytvořím symbolické proměnné všech stavů a použitých parametrů, pro případ kyvadla na vozíčku to vypadá takto:

% zavedeni symbolickych promennych vsech parametru a stavu vcetne vstupu
syms F m M L g b x phi dx dphi real
Is = 0;

přiřadím vstupní proměnnou:

% prirazeni vstupu
Vstupy = F;

zkopíruju z DynSystem.m model soustavy s vyjádřenými zrychleními stavů a pro stavy a vstupy provedu linearizaci:

% samotný výpočet derivací pro matice A,B:
JakobiA = jacobian(dStavy,[x dx phi dphi]);
JakobiB = jacobian(dStavy,F);

nadefinuju si rovnovážný bod soustavy

% rovnovazny bod
X0 = [0;0;0;0];
F0 = 0;

a dosadím do symbolických matic za stavy a vstupy:

% dosazeni rovnovazneho bodu do matic:
A=subs(JakobiA,[x; dx; phi; dphi; F],[X0;F0]);
B=subs(JakobiB,[x; dx; phi; dphi; F],[X0;F0]);

takto vytvořené matice A a B vložím do souboru LinSystem.m, ve kterém rovněž upravím část se vstupními parametry:

A = [0      1       0               0
     0      -b/M    -m*g/M          0
     0      0       0               1
     0      b/L/M   (m+M)*g/L/M     0];

 B = [0
    1/M
    0
    -1/L/M];

Dále zvolím výstup systému Y a vztah zase linearizuji a dosadím rovnovážný bod:

C = [1 0 L 0];
D = [0];

V poslední části dojde k výpočtu matice řiditelnosti, pozorovatelnosti a výpočtu vlastních čísel:

% riditelnost
R = ctrb(A,B);
% pozorovatelnost
O = obsv(A,C);
% stabilita
lambda = eig(A);

V další části souboru main.m je provedeno vyhodnocení modelu, jeho řiditelnost, pozorovatelnost a stabilita.

Úpravou prvního řádku souboru DynSystem.m je vytvořen soubor DynSystemSimulink.m, jehož první tři řádky jsou modifikovány pro použití v simulinkovské m-funkci (je nutno znát počet stavů, v našem příkladě 4):

function dStavy = DynSystemSimulink(VstupySimulink,parametry)
Stavy = VstupySimulink(1:4);
Vstupy = VstupySimulink(5);

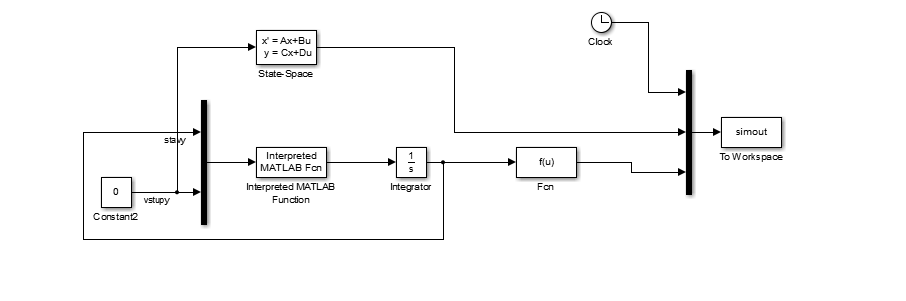
Nyní vytvoříme model v Simulinku, prázdný model vyvoláme příkazem >>simulink v okně matlabu. Modifikujeme hlavně buňku simulinkovského modelu označenou Fcn, která obsahuje funkci výstupní proměnné:

Model v simulinku je uložen jako MainSimulink.slx pro Matlab 2013a, pro starší verze jsou MainSimulink.mdl a MainSimulink2006.mdl. V souboru main.m je ukázáno, jak lze tento model spustit ze skriptu matlabu a vykreslení časové simulace linearizovaného a původního modelu:

sim('MainSimulink',0:1e-5:1);

figure;
plot(simout(:,1),simout(:,2));
figure;
plot(simout(:,1),simout(:,3));